机制设计:制定规则的科学
这门课程被大致组织为三个部分,每一部分都有各自的中心目标。下面是第一个目标:
课程目标一:理解如何在有策略性参与者的情况下,设计具有好的性能保证的系统。
我们通过一个警世故事开始。2012年的奥运会在伦敦举行。这场盛会所有运动项目中最大的丑闻之一发生在女子羽毛球这个项目上。这个丑闻并不涉及到任何失败的兴奋剂检测,而是一个没有仔细考虑动机(incentives)的失败了的赛制设计。
赛制设计在世界杯中很常见。参赛队伍被分为四组(A, B, C, D),每组有四支队伍。比赛分为两个阶段。第一阶段被称为循环赛。每支队伍和自己小组内的其他三支队伍进行一场比赛,但不和其他小组内的队伍进行比赛。每个小组的前两名会晋级到下一阶段,而后两门则被淘汰。在第二阶段,剩下的八支队伍会进行标准的淘汰赛(例如网球):有四场四分之一决赛(输者被淘汰),两场半决赛(输者会通过三四名的比赛决出铜牌)以及决赛(赢者得金牌,输者得银牌)。
在这样的赛制中,参赛者和奥运会组委会(以及球迷)的动机并不完全一致。球队想要什么?当然是尽可能拿金牌。奥运会组委会想要什么?他们似乎并没有仔细地想过这个问题,但事后看来很明显他们想要每一支队伍去尽力赢得每一场比赛。你可能会问,为什么会有队伍想要输掉一场比赛?确实,在淘汰赛阶段,输掉比赛就意味着淘汰出局,很明显赢比输好。
想要理解动机问题,我们需要解释在循环赛中胜出的八支队伍是如何在四分之一决赛中配对的。第一场四分之一决赛由A组的第一名对阵C组的第二名。类似地,第三场四分之一决赛由C组的第一名对阵A组的第二名。第二场和第四场四分之一决赛的安排也类似。多米诺效应出现在循环赛的最后一天。有一场令人失望的结果:丹麦组合Pederson和Juhl(PJ)击败了中国组合Qing和Wunlei(QW),因此PJ作为D组第一,QW作为D组第二晋级到淘汰赛。
第一场有争议的比赛发生在另一对中国组合,Xiaoli和Yang(XY)以及韩国组合Kyung-eun和Ha-na(KH)之间。这两支队伍在A组中都已经取得了两胜的战绩。因此,他们都将晋级到淘汰赛阶段,而这场比赛将决定这一组中的前两名的次序。问题来了:A组的第一名将会在半决赛中遇到可怕的QW组合(D组的第二名)。此时输掉比赛意味着最好只能拿铜牌。而A组的第二名直到决赛才会面对QW组合,此时可以保证拿铜牌。XY和KH组合都意识到了上面两种情况的差别足以重要,以至于要故意输掉比赛1。这种毫无吸引力的比赛场景导致了丑闻,嘲笑,并且最终导致了XY和KH组合失去了参赛资格。C组的另外两支队伍(来自印度尼西亚和另一支来自韩国的组合)也由于同样的原因采用了同样的策略而失去了资格2。
重点在于,在有策略性参与者的系统中,规则很重要。欠缺设计的系统会面临未曾预料的并且不被期待的结果。责任应该落在系统设计者身上,他们需要预料到策略性行为,而不是指望参与者能够与他们的自身利益作对。我们能够因为追求最大化赢得金牌的次序的行为而去责怪羽毛球员吗?引用Hartline和Kleinberg的话来说[1]:
“下一次我们为那些试图钻空子来违背规则制定者的意图的人们叹息时,不要问‘这些人出了什么问题?’而是应该问‘规则出了什么问题?’然后采用一种科学的途径来解决这些问题。”
现在已经有了关于规则制定的成熟领域:机制设计领域。这个领域的目标是设计规则使得参与者的策略行为导致令人满意的结果。我们后面会提到,机制设计的杀手级应用包括互联网搜索拍卖,无线频谱拍卖,医务人员和医院的匹配,儿童和学校的匹配以及肾交换市场。
我们会讨论机制设计中传统的经济学途径,也会介绍计算机科学对这一领域的几点补充,包括计算效率,近似最优和鲁棒性保证。
混乱代价(Price of Anarchy, POA):什么时候自私的行为是接近最优的
有时候你可能没有办法从头开始设计一个博弈的规则,而是想要了解一个“自然发生”的博弈,例如因特网或者道路网。
课程目标二:什么时候自私的行为本质上是无害的?
布雷斯悖论(Braess's Pradox)
作为开始,我们考虑布雷斯悖论(图1)[2]。有一个郊区s,一个火车站t,和一群固定数量的司机想要从s开车到t。如图1(a)所示,首先考虑s到t之间有两条互不干扰的路径,每一条路径都由一段宽路(不管有多少交通路,花费时间固定为1小时)和一条窄路(花费时间等于使用它的交通量)。这两条路径中的一条的两段路途加起来花费的时间都是1+x小时,其中x是使用这条路径的交通量。因此这两条路径是等价的,交通量在它们之间平分,在这种情况下,所有司机从s出发后花费90分钟到达目的地。
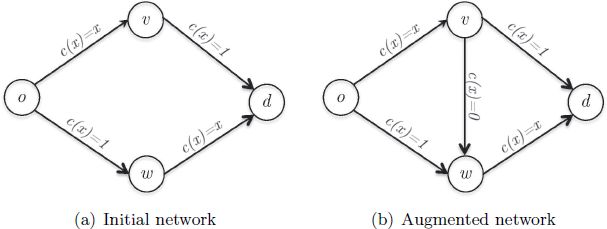
图1:布雷斯悖论。添加一条本来有用的边可能会反过来影响整个交通。
现在,考虑我们安装了一台能够允许司机瞬间从v移动到w的传送装置。新的网络表示在图1(b)中,其中传送装置用边(v,w)表示,并且花费的时间c(x)固定为0,与交通的拥塞无关。司机会如何反应?
我们不能期望之前的交通模式能够保持到新的网络,沿着新的路径的行程时间永远不会比沿着原来两条路径的时间多,而且如果有司机没有使用这条新路径的话是严格小于原来两条路径所需的时间。因此我们期待看到所有的司机都转移到新路径上。由于随之而来的边(s,v)和(w,t)上的交通拥堵,现在从s到t每个司机都需要花费2个小时的行程时间。布雷斯悖论表明原本有益的增加一条零开销的链路的行为最终对整个交通造成了负面的影响。
布雷斯悖论表明自私路由(selfish routing)并没有减少司机的行程时间,在有传送装置的网络中,一个利他的独裁者能够通过分配交通量的方式来使得每个司机的行程时间减少25%。我们定义混乱代价(price of anarchy, POA)为有策略性参与者的系统性能与最优的系统性能的比值。对于图1(b)中的网络而言就是2与的比值,即。
POA是首先由计算机科学家们定义和研究的。每一个经济学者和博弈论研究者都知道均衡一般是效率低下的,但直到21世纪前,不同的研究领域中也几乎没有量化这种低效率的尝试。
在我们对POA的研究中,首要目标是确认在哪些应用领域和条件下POA可以被确保接近于1,从而自私行为导致近似最优的结果。杀手级应用包括网络路由,调度,资源分配和简单拍卖设计。举例而言,网络容量的适当过度可以保证自私路由的POA接近于1。
线和弹簧
最后提一句,我们注意到自私路由也跟那些没有交通量的显式表示的系统有关。Cohen和Horowitz在一个由线和弹簧组成的机械结构中给出了布雷斯悖论的类似结果。
如图2中画出的装置所示,弹簧的一端接在一个固定的支撑点,另一端连着一根线,另一根相同的弹簧悬挂在线的自由端并且带着一个重物。最后,带着一定的松弛,一根线连接起支撑点和第二根弹簧的上端,另一根线连着第一根弹簧的底端和重物。假设弹簧是完全弹性的,伸长量与作用于弹簧上的力成线性关系。因此我们可以将线和弹簧组成的网络视作交通网,其中力代表了交通量而物理距离代表了开销。
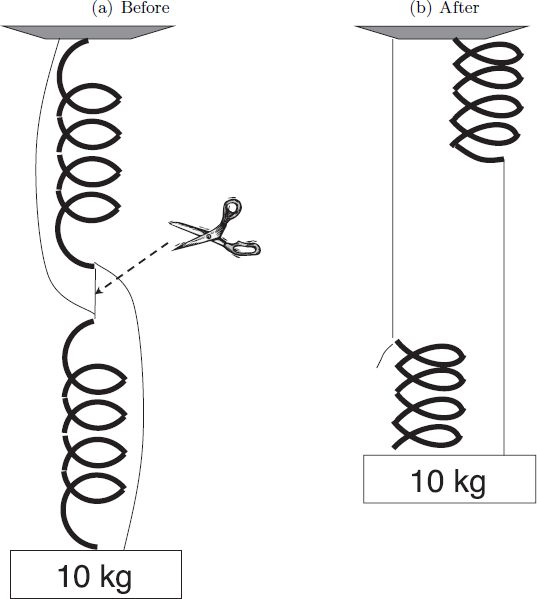
图2:线和弹簧。剪断紧绷的线会使重物上升。
通过对线和弹簧长度以及弹性系数的合理选择,这个机械网络的均衡位置可以表示在图2(a)中。可能难以想象的是,剪断紧绷的线会导致重物上升,正如图2(b)所示。对于这种现象的解释是这样的。一开始,两根弹簧是串联相接的,每根弹簧都承载了全部的重量从而拉长到了最大长度。剪断紧绷的线后,两根弹簧变成了并联。每根弹簧只承载了一半的重量,从而只延伸了之前长度的一半。重物的上升跟从图1(b)中删除零开销的边从而得到图1(a)网络的自私结果带来的提高一样。
这种构造并不仅仅是理论上的,在YouTube上你可以找到由CS364A之前的学生实施的(为了获得额外加分)关于布雷斯悖论的一些物理演示。
均衡的复杂度:策略性局中人是如何学习的?
一些博弈很容易进行。举例而言,在布雷斯悖论的第二个网络中(图1(b))中,使用传送装置是每一个个体的无脑选择。因此无论其他司机怎么做,它都是最好的路径。在很多其他博弈中,例如下一讲中要提到的最高价拍卖,搞清楚如何博弈会变得难很多。
课程目标三:策略性局中人如何到达均衡?(或者他们会到达均衡吗?)
非正式的,均衡是系统的一种“稳定状态”,其中假设其他都保持一样的话,每一个参与者会希望保持原样。希望你还没有从电影《美丽心灵》中学到纳什均衡的定义。
在大多数博弈中,最佳行为取决于其他局中人会怎么做。剪刀石头布,如下表所示的“双矩阵”形式,是一个标准的例子。
| 石头 | 布 | 剪刀 | |
|---|---|---|---|
| 石头 | 0, 0 | -1, 1 | 1, -1 |
| 布 | 1, -1 | 0, 0 | -1, 1 |
| 剪刀 | -1, 1 | 1, -1 | 0, 0 |
一个局中人选择一行,另一个局中人选择一列。对应的矩阵条目分别是行和列局中人的收益。
在剪刀石头布的博弈中肯定没有“确定性的均衡”:无论现在的状态如何,至少会有一个局中人可以通过单方面的变动获益。
一个重要的想法,主要由冯诺依曼提出,是允许随机的(或,混合的)策略。(在一个类似剪刀石头布的博弈中,从你的角度看,你的对手实际上是随机的。)如果在简单石头布中,两个局中人都均匀地采用随机的策略,那么没有局中人能够通过单方面的变动获益。因为,每一种单方面的变动都不会给变动者带来期望收益。具有这样性质的一个概率分布对被称作(混合策略)纳什均衡。
值得注意的是,通过随机化,每一个博弈都至少拥有一个纳什均衡:
纳什定理('51):每一个双矩阵博弈都有纳什均衡。
纳什定理对于更一般意义上的拥有有限数量的局中人的博弈也成立。
另一个我们课上会提到的好消息是:如果一个双矩阵博弈是零和的――意味着每一个条目中的收益对的和为零,例如剪刀石头布――那么一个纳什均衡可以在多项式时间内计算出来。这可以通过线性规划,或者如果可以允许少量误差的话,通过迭代学习算法。这些算法的结果验证了纳什均衡可以作为零和博弈中行为的很好预测。
在更近些时候(最近十年),计算机科学贡献了一个重要的否定性结果:在适当的复杂度假设下,没有多项式时间的算法可以计算一般的(非零和)博弈的纳什均衡[3, 4]。尽管这个问题不是NP难的(除非NP=coNP),它有时候被称作“PPAD难”,我们会在后面的课程中解释。
这个困难结果是有趣的,因为两个不同的原因。从技术角度讲,它表明了计算纳什均衡是一个基本的具有“中等”难度的计算问题(类似质因数分解和图的同构)――不太可能属于P或者NP完全问题。从概念角度讲,均衡概念的许多解释都会涉及到某个人――参与者或设计者――决定均衡。举例来说,市场隐形地计算一个重要问题的解决方案的想法至少可以回溯到亚当斯密提出的有关看不见的手的概念[5]。如果各方都是有限理性的,那么只有当均衡能够通过合理的代价计算得到的话才可以被解读为一个可信的预测。计算上严格困难的结果让人怀疑均衡概念的预测能力(最早从Rabin[6]就开始有的批评)。尽管计算困难肯定不是纳什均衡概念面临的第一个困难,但它肯定是一个理想的理论计算机科学研究的问题。从这个角度出发,我们也得到了研究一些“简单的”均衡概念的新的动机,例如相关均衡和粗的相关均衡。
计算机科学家带来了什么?
当然,现在经济学中已经有了大量关于机制设计和均衡的文献。在这门课程中,我们将看到计算机科学家是如何通过一系列新的途径补充了这方面的研究。在我们研究的这个话题上传统的经济学途径倾向于专注在“贝叶斯”(即,平均情况)分析,强调精确解和描述,而且经常忽略计算难度。计算机科学提供了讨论计算复杂度的语言;推广了研究精确解不实际或不可解的模型广泛使用的近似界限;并鼓励更加健壮的性能保证。
目标读者
这些课件假设读者有一个本科阶段的理论计算机科学背景――基本算法和NP完备性。它们并不要求任何博弈论或经济学方面的背景(相反地,这门课程也无法替代传统的博弈论或微观经济学)。这种层次的设定是为了更加适合具有一定理论基础的硕士生和一年级博士生。
脚注:
1 事后证明比起丹麦组合PJ,这两支队伍更加害怕中国组合QW是有道理的,PJ在四分之一决赛中被淘汰,而QW赢得了金牌。
2 如果你觉得难以想象一场两队都想输的羽毛球比赛的场景,我建议你去YouTube上寻找相关的视频。
参考文献
[1] J. D. Hartline and R. D. Kleinberg. The badminton and the science of rule making. The Huffington Post, August 13 2012. http://www.huffingtonpost.com/jason-hartline/badminton-and-the-science-of-rule-makingb1773988.html.
[2] Braess D. Über ein Paradoxon aus der Verkehrsplanung[J]. Mathematical Methods of Operations Research, 1968, 12(1):258-268.
[3] Xi Chen and Xiaotie Deng. Settling the complexity of two-player nash equilibrium. In FOCS, volume 6, page 47th, 2006.
[4] Constantinos Daskalakis, Paul W Goldberg, and Christos H Papadimitriou. The complexity of computing a nash equilibrium. SIAM Journal on Computing, 39(1):195-259, 2009.
[5] Adam Smith and Joseph Shield Nicholson. An Inquiry Into the Nature and Causes of the Wealth of Nations. T. Nelson and Sons, 1887.
[6] Michael O Rabin. Effective computability of winning strategies. Contributions to the Theory of Games, 3(39):147-157, 1957.
[7] Joel E Cohen and Paul Horowitz. Paradoxical behaviour of mechanical and electrical networks. 1991.
[8] Tim Roughgarden. The price of anarchy is independent of the network topology. Journal of Computer and System Sciences, 67(2):341-364, 2003.